Distances

15.4. Мера расстояния и мера сходства

Наряду с приведенными корреляционными коэффициентами, SPSS дополнительно предлагает расчет ряда мер расстояния и мер сходства. Так, к примеру, реализован расчет многочисленных мер сходства при анализе взаимосвязи между дихотомическими переменными. Некоторые статистические процедуры, такие как факторный анализ, кластерный анализ, многомерное масштабирование, построены на применении этих мер, а иногда сами представляют добавочные возможности для вычисления мер подобия. Если Вы во время выполнения этих процедур захотите использовать какую-либо меру, не предусмотренную в выбранной процедуре, то следует воспользоваться дополнительными возможностями, предоставляемыми SPSS.

В качестве примера возьмем анкету, которая будет рассматриваться в главе 21. Она посвящена исследованию степени любознательности опрашиваемых.

• Откройте файл neugier.sav.

• Выберите в меню Analyze... (Анализ) ► Correlate... (Корреляция) ► Distances... (Расстояния). Появится диалоговое окно Distances... (Расстояния).

В этом диалоговом окне Вы можете организовать расчет расстояния между наблюдениями или между переменными, а также выбрать тип рассчитываемой меры мера отличия или мера подобия). Щелчком на кнопке Measures... (Меры) можно выбрать формулу вычисления меры расстояния для интервальных или дихотомических (бинарных) переменных. В основу расчета мер отличия могут быть также положены и частоты.

Все меры отличия и сходства для переменных, принадлежащих к интервальной шкале, будут рассмотрены в главе 20.3. Эти меры являются важным элементом кластерного анализа. Ниже приведены формулы для мер сходства между бинарными (дихотомическими) переменными, принадлежащими к интервальной шкале. Символами а, b, с и d обозначены частоты, находящиеся в ячейках таблицы 2x2 (четырёхполевой таблицы). В случае необходимости, более подробное объяснение этих формул Вы найдёте в главе 20.3.3.

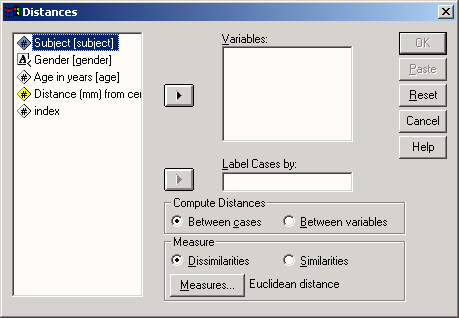
Рис. 15.4: Диалоговое окно Distances... (Расстояния).

• Рассел и Рао (Russel and Rao)

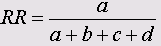
• Простое согласование

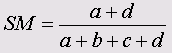
• Джаккард (Jaccard)

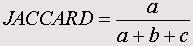
• Игральная кость

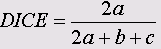
• Роджерс и Танимото (Rogers and Tanimoto)

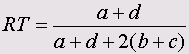
• Соукал и Снис 1 (Sokal and Sneath)

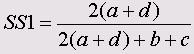
• Соукал и Снис 2

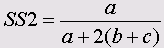
• Соукал и Снис 3

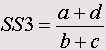
• Кульчинский 1 (Kulczynski)

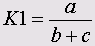
• Кульчинский 2

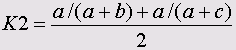
• Соукал и Снис 4

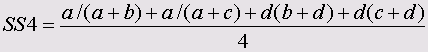
• Хаманн (Hamann)

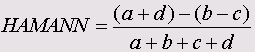
• Лямбда

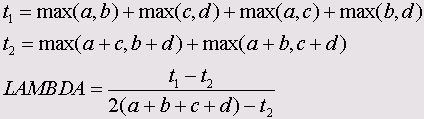
• D Андерберга (Anderberg)

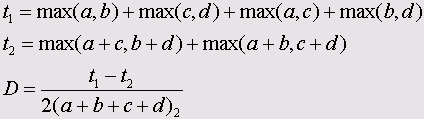
• Y Юля

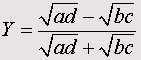
• Q Юля

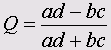
• Очиаи (Ochiai)

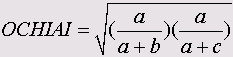
• Соукал и Скис 5

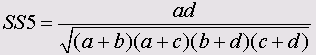
• 4 точечная µ-корреляция

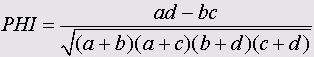
• Дисперсия

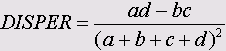
Два следующих примера помогут разобраться в особенностях работы с мерами расстояния.

Пример первый: сходства между дихотомическими переменными.

• Создайте сначала таблицу сопряженности для переменных item3 и item14. Эти переменные соответствуют ответам на вопросы "Считаете ли Вы, что развитие космонавтики необходимо?" и соответственно "Согласились бы Вы предоставить себя в распоряжение учёным для научных экспериментов?" (с кодировками 1 = да и 2 = нет).

Частоты в таблице 2x2 распределились следующим образом:

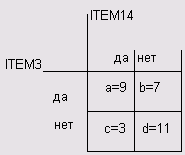
Рис. 15.5: Частоты в таблице 2x2

• Выберите в меню Analyze... (Анализ) ► Correlate... (Корреляция) ► Distances... (Расстояния)

• Перенесите переменные item3 и item14 в поле тестируемых переменных.

• Активируйте расчёт расстояний Between Variables (Между переменными) и в качестве типа меры выберите Similarities... (Подобия).

• Щёлкните на кнопке Measures... (Меры) и, в открывшемся диалоговом окне, активируйте Binary (Бинарные). Оставьте предварительную установку мер вычисления по методу Рассела и Рао.

• Так как в приведенном примере отрицательному ответу присвоен код 2, а в предварительных установках предусмотрен 0, то Вам необходимо откорректировать это значение в поле Absent (Отсутствует).

• Покиньте диалоговое окно мер нажатием Continue (Далее) и в главном диалоговом окне начните расчёт щелчком на ОК.

В результате Вы получите значение меры подобия равное 0,3. Оно определяется как частное от деления частоты а на сумму всех четырёх частот:

Proximity Matrix (Матрица близости)

This is a similarity matrix (Это матрица подобия) ;

Пример второй: расчёт корреляционной матрицы 2x2 в качестве базиса для факторного анализа

Мы хотим рассчитать корреляционную матрицу для восемнадцати переменных item1 - item18 с применением четырёхточечная корреляция фи. В этом случае корреляционную матрицу можно использовать в качестве базиса для факторного анализа. Для решения этой задачи нам предстоит поработать с программным синтаксисом SPSS.

• Перенесите переменные item1 - item18 в поле тестируемых переменных.

• Активируйте расчёт расстояний Between Variables (Между переменными) и в качестве типа меры выберите Similarities... (Подобия).

• Откройте щелчком на кнопке Measures... (Меры) соответствующее диалоговое окно, активируйте в нём Binary (Бинарные) и присвойте параметру Absent (Отсутствует) код 2. В заключении вместо меры по Расселу и Рао выберите 4 точечную µ-корреляцию.

• При помощи щелчка на Continue (Далее) вернитесь в основное диалоговое окно, после прохождения кнопки Paste... (Вставить) просмотрите синтаксис команд.

• Внесите в синтаксис следующие корректировки:

PROXIMITIES
item1 item2 item3 item4 item5 item6 item7 item8 item9 item10 item11 item12 item13 item14 item15 item16 item17 item18
/VIEW=VARIABLE
/MEASURE= PHI (1,2)
/MATRIX=OUT(*).
RECODE rowtype_ ("PROX"='CORR').
FACTOR /MATRIX=IN(COR=*).

• Начните расчёт при помощи символа Syntax-Start (Синтаксис-Начать).

В окне просмотра появятся результаты факторного анализа, а в окне редактора данных будет показана корреляционная матрица.