16.8 Приближение с помощью кривых
При помощи этого пункта меню можно строить графики реального течения наблюдаемых процессов и приближать их при помощи аппроксимационных кривых. Для этого в ваше распоряжение предоставляется, в общей сложности, одиннадцать различных типов кривых. В большинстве случаев речь здесь будет идти о временных рядах.
В качестве примера рассмотрим изменение зарплаты в Федеративной республике Германии с 1950 года по 1988, описываемое так называемым индексом действительной зарплаты. Его можно получить при помощи соотнесения текущего годового уровня зарплаты к уровню к 1980 году, для которого значение индекса принимается равным 100.
|
Год
|
Индекс действительной зарплаты
|
|
1950
|
28,6
|
|
1960
|
46,9
|
|
1965
|
63,0
|
|
1970
|
80,4
|
|
1975
|
87,9
|
|
1980
|
100,0
|
|
1981
|
98,2
|
|
1982
|
96,5
|
|
1983
|
96,0
|
|
1984
|
96,9
|
|
1985
|
98,0
|
|
1986
|
101,2
|
|
1987
|
104,5
|
|
1988
|
107,6
|
Эти данные находятся в файле lohasav. В файле также находится и ещё одна, третья, переменная, которая отражает разность между текущим значением года и 1949 годом. Эта переменная принимает значения от 1 до 39 и указывает на количество лет, прошедших с 1949 года.
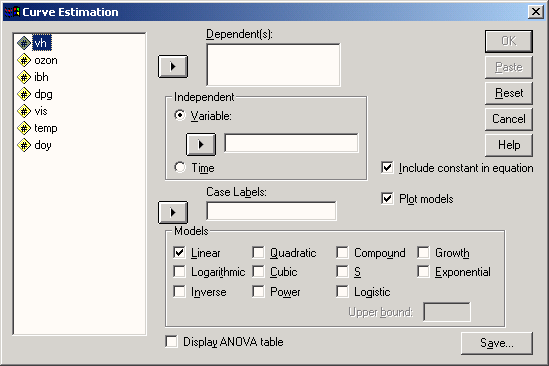
Рис. 16.24: Диалоговое окно Curve Estimation (Подгонка кривых)
Откроется диалоговое окно Curve Estimation (Подгонка кривых), в котором можно выбрать одну из одиннадцати различных моделей.
Предлагаемым моделям соответствуют следующие формулы:
|
Молель
|
Формула
|
|
Линейная
|
у= b0+ b1хX
|
|
Логарифмическая
|
у= b0+ b1х ln(х)
|
|
Обратная
|
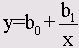
|
|
Квадратичная
|
у= b0+ b1хX + b2хX2
|
|
Кубическая
|
у= b0+ b1хХ + b2хX2 + b3хX3
|
|
Степенная
|
y= b0хXb1
|
|
Показательная (комбинированная)
|
y= b0 *
b1
|
|
S
|
у= е^(b0+b1xX)
|
|
Логистическая
|
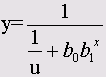
|
|
Рост
|
у= е^(b0+b1xX)
|
|
Экспоненциальная
|
y=b0 х
е^(b1xt)
|
Для логистической модели необходимо предварительно задать параметр и, который задается непосредственно в диалоговом окне Curve Estimation (Подгонка кривых) в
качестве верхнего предела. Задачей программы является определение коэффициентов
b0, b1, b2 и b3.
В поле для меток наблюдений (Case labels) можете указать некоторую переменную для описания данного наблюдения, которая затем будет появляться в режиме выбора точек (см. гл. 22.8.1) на построенном графике (см. рис. 16.25).
-
Перенесите переменную lohn в поле для зависимых переменных, а переменную anz в поле для независимых переменных.
-
Произведём оценку при помощи квадратичной функции; деактивируйте линейную модель и отметьте вместо неё квадратичную модель.
Активирование опции Time (Время) имеет смысл только тогда, когда анализируемые переменные представлены в виде временных рядов с одинаковыми интервалами.
-
Затем щёлкните на кнопке Save (Сохранение) и в появившемся диалоговом окне выберите опцию, с помощью которой прогнозируемые значения переменной будут сохранены в исходном файле данных.
-
Вернувшись в первое диалоговое окно, начните расчёт нажатием ОК.
Вывод результатов производится в старой табличной форме. Самыми важными показателями
являются:
Independent: ANZ
Dependent Mth Rsq d.f. F Sigf b0 b1 b2
LOHN QUA ,979 11 251,10 ,000 22,5918 3,0615 -,0242
Эта таблица содержит значения коэффициентов а,
b1, и b2. К данным исходного файла была добавлена переменная
fit_1, которая содержит прогнозируемые значения, найденные на основе рассчитанных коэффициентов. Далее в окне просмотра появляется график, на котором отображаются кривые, соответствующие изменению наблюдаемых и спрогнозированных значений.
Приближение с помощью выбранной кривой, как кажется, удалось довольно не плохо. В противном случае можно было бы применить и другие модели, для использования которых, конечно же, не помешал бы некоторый опыт в области подобных криволинейных приближений.
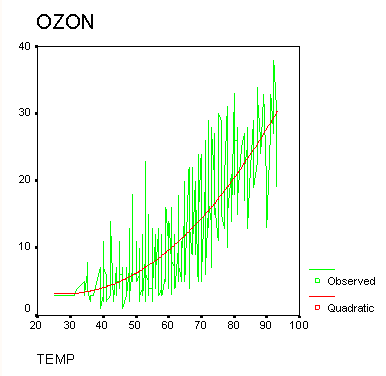
Рис 16.25: Наблюдаемая и оценочная кривая
|