Svaru novērtējums

16.9 Взвешенное оценивание (оценка с весами)

В линейном регрессионном анализе, рассмотренном до настоящего времени, все наблюдения входят в модель равнозначно. При этом, исходной предпосылкой является тот факт, что все наблюдения должны иметь одинаковую дисперсию.

Если это условие не выполняется и дисперсия увеличивается с ростом значения независимой переменной, то отдельные точки можно взвесить так, чтобы наблюдения с большой дисперсией имели меньшее влияние.

В качестве примера рассмотрим тест, проверяющий знания детей в области географии. Дети в возрасте от 3 до 14 лет должны были в течение двух минут назвать как можно больше городов Германии. Результаты теста сведены в нижеследующей таблице, причём количество детей в каждой возрастной группе варьируется от двух до пяти:

Эти данные для сорока детей в общей сложности хранятся в переменных alter (возраст) и staedte (города), которые содержатся в файле snamen.sav.

•  Откройте файл snamen.sav.

•  Выберите в меню Graphs (Графики) Scatterplot... (Диаграмма рассеяния)

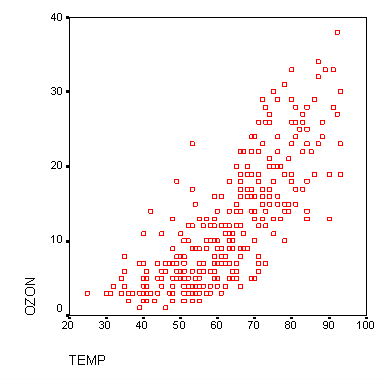
Рис. 16.26: Диаграмма рассеяния

•  Отметьте и постройте простую диаграмму рассеяния с переменной alter по оси абсцисс и переменной staedte пo оси ординат.

Вы увидите, что с ростом возраста растёт не только количество названных городов, но и рассеяние, то есть дисперсия, становится больше.

•  В соответствии с описанием из главы 16.1 проведите линейный регрессионный анализ, причём переменной staedte присвойте статус зависимой переменной, а переменной alter — независимой переменной.

•  Вы получите следующие результаты:

Model Summary (Сводная таблица по модели)

a. Predictors: (Conslant), Alter (Bлияющие переменные: (Константа), возраст)

Коэффициент корреляции равен 0,879, а мера определённости 0,772.

В данном примере мы имеем дело с группами случаев, разделёнными по годам возраста, для которых независимая переменная имеет всегда одно и то же значение. Исходя из значений зависимой переменной сопоставленных каждому случаю, можно определить дисперсию; обратное значение этой дисперсии применяется обычно в качестве весового фактора для соответствующего случая.

Если подобной группировки данных нет, то пытаются выявить такую связь между дисперсией и переменной, чтобы степень дисперсии была пропорциональна значению данной переменной. При поиске так называемых весовых переменных речь идет о независимой переменной или, если их много, — об одной из независимых переменных. В приведенном примере такой переменной, очевидно, является независимая переменная alter, по которой и можно проследить изменение дисперсии.

Целью анализа сначала является определение наилучшей возможной степени р. а затем подсчёт веса для каждого случая, причём вес для значения переменной х определяется как

1/х^p

•  Выберите в меню Analyze (Анализ) Regression.. .(Регрессия) Weight Estimation... (Взвешенное оценивание)

Откроется диалоговое окно Weight Estimation (Взвешенное оценивание).

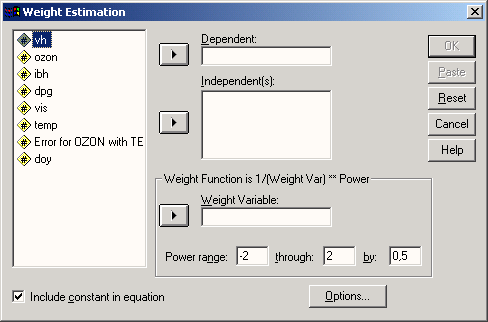
Рис. 16.27: Диалоговое окно Weight Estimation (Весовая цепка)

•  Перенесите переменную staedte в поле зависимых переменных, а переменную alter в поля для независимых и для весовых переменных. Согласно с установками по умолчанию оптимальная степень вычисляется в пределе от —2 до 2 с шагом 0,5; измените шаг на 0,2.

•  Щёлкните на кнопке опций и в появившемся диалоговом окне активируйте опцию Save best weight as new variable (Сохранить лучший вес, как новую переменную).

Результаты расчёта, вывод которых производится в старой табличной форме, выглядят следующим образом:

Оптимальная степень оценивается при помощи логарифма функции правдоподобия; в данном случае максимальное значение получается при значении степени равном 1,4. Это значение используется для определения веса для каждого случая. К примеру, для трёхлетнего ребёнка вес равен

1/(3^1,4)=0,2148 

Весовые показатели были добавлены в исходный файл под переменной с именем wgt_1. Затем повторно был выполнен расчёт регрессии. Корреляционный коэффициент при этом возрос до 0,90081, а мера определённости до 0,81146. Хотя эти изменения, а также изменение рассчитанных коэффициентов регрессии и констант незначительны, зато стала намного меньше соответствующая им стандартная ошибка.