16.1 Простая линейная регрессия
Рис. 16.1: Вспомогательное меню Regression (Регрессия)
При изучении линейного регрессионного анализа снова будут проведено различие между простым анализом (одна независимая переменная) и множественным анализом (несколько независимых переменных).
Никаких принципиальных отличий между этими видами регрессии нет, однако простая линейная регрессия является простейшей и применяется чаще всех остальных видов.
Этот вид регрессии лучше всего подходит для того, чтобы продемонстрировать основополагающие принципы регрессионного анализа. Рассмотрим пример из раздела
корреляционный анализ с зависимостью показателя холестерина спустя один месяц после начала лечения от исходного показателя.
Можно легко заметить очевидную связь: обе переменные развиваются в одном направлении и множество точек, соответствующих наблюдаемым значениям показателей,
явно концентрируется (за некоторыми исключениями) вблизи прямой (прямой регрессии). В таком случае говорят о линейной связи.
у = b • х + а,
где b — регрессионные коэффициенты, a — смещение по оси ординат (OY).
Смещение по оси ординат соответствует точке на оси Y (вертикальной оси), где прямая регрессии пересекает эту ось. Коэффициент регрессии b через соотношение:
b = tg(a) - указывает на угол наклона прямой.
При проведении простой линейной регрессии основной задачей является определение параметров b и а. Оптимальным решением этой задачи является такая прямая,
для которой сумма квадратов вертикальных расстояний до отдельных точек данных является минимальной.
Если мы рассмотрим показатель холестерина через один месяц (переменная chol1) как зависимую переменную (у), а исходную величину как независимую переменную (х),
то тогда для проведения регрессионного анализа нужно будет определить параметры соотношения:
chol1 = b • chol0 + a
После определения этих параметров, зная исходный показатель холестерина, можно спрогнозировать показатель, который будет через один месяц.
Расчёт уравнения регрессии
Откройте файл hyper.sav.
Выберите в меню Analyze... (Анализ) ► Regression...(Регрессия) ► Linear... (Линейная). Появится диалоговое окно Linear Regression (Линейная регрессия). Перенесите переменную chol1 в поле для зависимых переменных и присвойте переменной chol0 статус независимой переменной. Ничего больше не меняя, начните расчёт нажатием ОК.
Рис.16.2: Диалоговое окно Линейная регрессия
Вывод основных результатов выглядит следующим образом:
Model Summary (Сводная таблица по модели)
| Model (Модель) |
R |
R Square (R-квадрат) |
Adjusted R Square (Скорректир. R-квадрат) |
Std. Error of the Estimate (Стандартная ошибка оценки) |
| 1 |
,861а |
,741 |
,740 |
25,26 |
а. Predictors: (Constant), Cholesterin, Ausgangswert (Влияющие переменные: (константы), холестерин, исходная величина)
ANOVA b
| Model (Модель) |
|
Sum of Squares (Сумма Квадратов) |
df |
Mean Square (Среднее значение квадрата) |
F |
Sig. (Значимость) |
| 1 |
Regression (Регрессия) |
314337,948 |
1 |
314337,9 |
492,722 |
,000a |
| Residual (Остатки) |
109729,408 |
172 |
637,962 |
|
|
| Total (Сумма) |
424067,356 |
173 |
|
|
|
a. Predictors: (Constant), Cholesterin, Ausgangswert (Влияющие переменные: (константа), холестерин, исходная величина).
b. Dependent Variable: Cholesterin, nach 1 Monat (Зависимая переменная холестерин через 1 месяц)
Coefficients (Коэффициенты) а
| Model (Модель) |
|
Unstandardized Coefficients
(Не стандартизированные коэффициенты) |
Standardized Coefficients (Стандартизированные коэффициенты) |
t |
Sig. (Значимость) |
| B |
Std: Error
(Станд. ошибка) |
ß (Beta) |
| 1 |
(Constant) (Константа) |
34,546 |
9,416 |
|
3,669 |
,000 |
| Cholesterin, Ausgangswert |
,863 |
,039 |
,861 |
22,197 |
,000 |
a. Dependent Variable (Зависимая переменная)
Рассмотрим сначала нижнюю часть результатов расчётов. Здесь выводятся коэффициент регрессии b и смещение по оси ординат а под именем "константа".
То есть, уравнение регрессии выглядит следующим образом:
chol1 = 0,863 • chol0 + 34,546
Если значение исходного показателя холестерина составляет, к примеру, 280, то через один месяц можно ожидать показатель равный 276.
Частные рассчитанных коэффициентов и их стандартная ошибка дают контрольную величину Т; соответственный уровень значимости относится к существованию ненулевых коэффициентов регрессии.
Значение коэффициента ß будет рассмотрено при изучении многомерного анализа.
Средняя часть расчётов отражает два источника дисперсии: дисперсию, которая описывается уравнением регрессии (сумма квадратов, обусловленная регрессией) и дисперсию,
которая не учитывается при записи уравнения (остаточная сумма квадратов). Частное от суммы квадратов, обусловленных регрессией и остаточной суммы квадратов называется
"коэфициентом детерминации". В таблице результатов это частное выводится под именем "R-квадрат". В нашем примере мера определённости равна:
314337,948 / 424067,356 = 0,741
Эта величина характеризует качество регрессионной прямой, то есть степень соответствия между регрессионной моделью и исходными данными. Мера определённости всегда лежит в диапазоне от 0 до 1.
Существование ненулевых коэффициентов регрессии проверяется посредством вычисления контрольной величины F, к которой относится соответствующий уровень значимости.
В простом линейном регрессионном анализе квадратный корень из коэфициента детерминации, обозначаемый "R", равен корреляционному коэффициенту Пирсона. При множественном анализе эта величина менее наглядна,
нежели сам коэфициент детерминации. Величина "Cмещенный R-квадрат" всегда меньше, чем несмещенный. При наличии большого количества независимых переменных,
мера определённости корректируется в сторону уменьшения. Принципиальный вопрос о том, может ли вообще имеющаяся связь между переменными рассматриваться как линейная, проще и нагляднее всего решать,
глядя на соответствующую диаграмму рассеяния. Кроме того, в пользу гипотезы о линейной связи говорит также высокий уровень дисперсии, описываемой уравнением регрессии.
И, наконец, стандартизированные прогнозируемые значения и стандартизированные остатки можно предоставить в виде графика. Вы получите этот график, если через кнопку Plots...(Графики)
зайдёте в соответствующее диалоговое окно и зададите в нём параметры *ZRESID и *ZPRED в качестве переменных, отображаемых по осям у и х соответственно.
В случае линейной регрессии остатки распределяются случайно по обе стороны от горизонтальной нулевой линии.
Сохранение новых переменных
Многочисленные вспомогательные значения, рассчитываемые в ходе построения уравнения регрессии, можно сохранить как переменные и использовать в дальнейших расчётах.
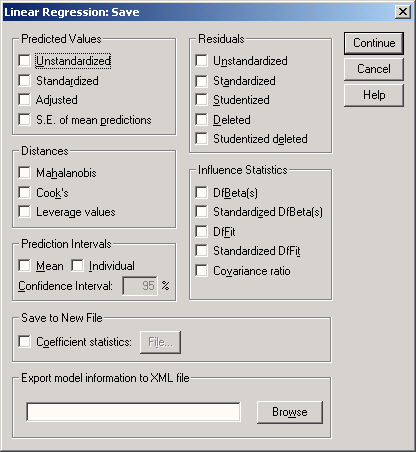
Рис. 16.3: Диалоговое окно Линейная регрессия: Сохранение
Интересными здесь представляются опции Standardized (Стандартизированные значения) и Unstandardized (Нестандартизированные значения), которые находятся под рубрикой Predicted values
(Прогнозируемые величины опции). При выборе опции Не стандартизированные значения будут рассчитывается значения у, которое соответствуют уравнению регрессии.
При выборе опции Стандартизированные значения прогнозируемая величина нормализуется. SPSS автоматически присваивает новое имя каждой новообразованной переменной, независимо от того,
рассчитываете ли Вы прогнозируемые значения, расстояния, прогнозируемые интервалы, остатки или какие-либо другие важные статистические характеристики. Нестандартизированным значениям
SPSS присваивает имена pre_1 (predicted value), pre_2 и т.д., а стандартизированным zpr_l.
Щёлкните в диалоговом окне Linear Regression: Save (Линейная регрессия: Сохранение) в поле Predicted values (Прогнозируемые значения) на опции Unstandardized (Нестандартизированные значения). Подтвердите нажатием Continue (Далее) и в заключение ОК.
В редакторе данных будет образована новая переменная под именем рrе_1 и добавлена в конец списка переменных в файле. Для объяснения значений, находящихся в переменной рrе_1,
возьмём случай 5. Для случая 5 переменная рrе_1 содержит нестандартизированное прогнозируемое значение 263,11289. Это прогнозируемое значение слегка отличается в сторону увеличения от
реального показателя содержания холестерина, взятого через один месяц (chol1) и равного 260. Нестандартизированное прогнозируемое значение для переменной chol1,
так же как и другие значения переменной рге_1, было вычислено исходя из соответствующего уравнения регрессии.
Если мы в уравнение регрессии:
chol1 = 0,863 • chol0 + 34,546
подставим исходное значение для chol0 (265), то получим: chol1 = 0,863 • 265 + 34,546 = 263,241
Небольшое отклонение от значения, хранящегося в переменной рге_1 объясняется тем, что SPSS использует в расчётах более точные значения, чем те, которые выводятся в окне просмотра результатов.
Добавьте для этого в конец файла hyper.sav, ещё два случая, используя фиктивные значения для переменной chol0.
Пусть к примеру, это будут значения 282 и 314.
Мы исходим из того, что нам не известны значения показателя холестерина через месяц после начала лечения, и мы хотим спрогнозировать значение переменной chol1.
В конце списка переменных добавится переменная рге_2. Для нового добавленного случая (№175) для переменной chol1 будет предсказано значение 277,77567, а для случая №176 — значение 305,37620.
Построение регрессионной прямой
Чтобы на диаграмме рассеяния изобразить регрессионную прямую, поступите следующим образом:
Выберите в меню следующие опции Graphs ... (Графики) / Scatter plots... / Диаграммы рассеяния. Откроется диалоговое окно Scatter plots... (Диаграмма рассеяния) - (рис. 16.4). 
Рис. 16.4: Диалоговое окно Scatter plots... (Диаграмма рассеяния)
В диалоговом окне Scatter plots...(Диаграмма рассеяния) оставьте предварительную установку Simple (Простая) и щёлкните на кнопке Define (Определить).
Откроется диалоговое окно Simple Scatter plot (Простая диаграмма рассеяния) (рис. 16.5). 
Рис. 16.5: Диалоговое окно Simple Scatterplot (Простая диаграмма рассеяния).
Перенесите переменную chol1 в поле оси Y, а переменную chol0 в поле оси X. Подтвердите щелчком на ОК. В окне просмотра результатов появится диаграмма рассеяния (рис. 16.6). 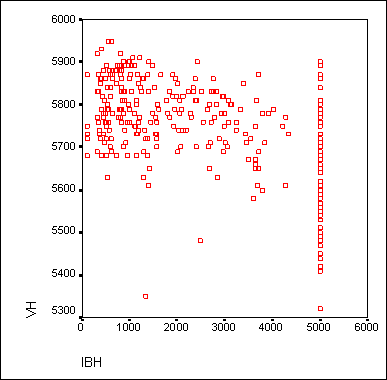
Рис. 16.6: Диаграмма рассеяния в окне просмотра
Щёлкните дважды на этом графике, чтобы перенести его в редактор диаграмм. Выберите в редакторе диаграмм меню Chart... (Диаграмма) / Options... (Опции). Откроется диалоговое окно Scatterplot Options (Опции для диаграммы рассеяния) (рис. 16.7). 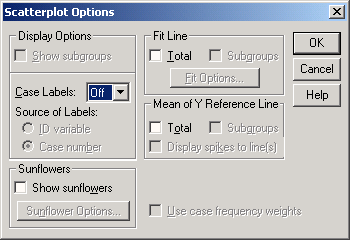
Рис. 16.7: Диалоговое окно Scatterplot Options (Опции для диаграммы рассеяния)
-
В рубрике Fit Line (Приближенная кривая) поставьте флажок напротив опции Total (Целиком для всего файла данных) и щёлкните на кнопке Fit Options (Опции для приближения).
Откроется диалоговое окно Scatterplot Options: Fit Line (Опции для диаграммы рассеяния: приближенная кривая) (см. рис. 16.8).
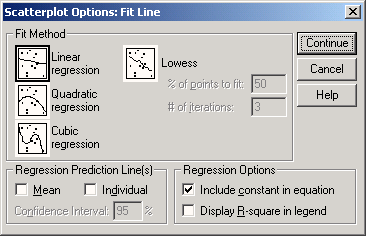
Рис. 16.8: Диалоговое окно Scatterplot Options: Fit Line (Опции для диаграммы рассеяния:
Подтвердите предварительную установку Linear Regression (Линейная регрессия) щелчком Continue (Далее) и затем на ОК. Закройте редактор диаграмм и щёлкните один раз где-нибудь вне графика. Теперь в диаграмме рассеяния отображается регрессионная прямая (рис. 16.9).
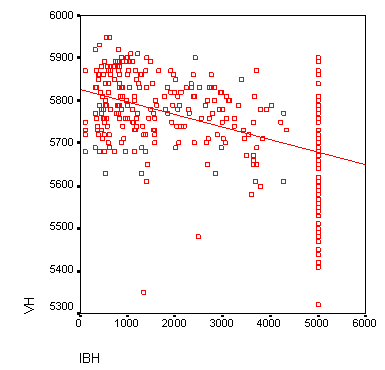
Рис. 16.9: Диаграмма рассеяния с регрессионной прямой
Выбор осей
Для диаграмм рассеяния часто оказывается необходимой дополнительная корректировка осей. Продемонстрируем такую коррекцию при помощи одного примера. В файле
raucher.sav находятся десять фиктивных наборов данных. Переменная konsum указывает на количество сигарет, которые выкуривает один человек в день,
а переменная puls на количество времени, необходимое каждому испытуемому для восстановления пульса до нормальной частоты после двадцати приседаний. Как было показано ранее,
постройте диаграмму рассеяния с внедрённой регрессионной прямой.
В диалоговом окне Simple Scatterplot (Простая диаграмма рассеяния) перенесите переменную puls в поле оси Y, а переменную konsum — в поле оси X. После соответствующей обработки данных в окне просмотра появится диаграмма рассеяния, изображённая на рисунке 16.10.
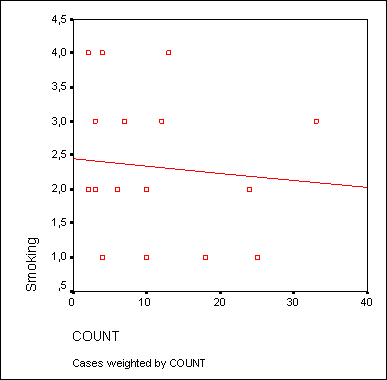
Рис. 16.10: Диаграмма рассеяния с регрессионной прямой до коррекции осей
Так как никто не выкуривает минус 10 сигарет в день, точка начала отсчёта оси X является не совсем корректной. Поэтому эту ось необходимо откорректировать.
Дважды щёлкните на графике и в меню редактора диаграмм вберите опции Chart... (Диаграмма) / Axis... (Оси). Откроется диалоговое окно Axis Selection (Выбор оси) (рис. 16.11). 
Рис. 16.11: Диалоговое окно Axis Selection (Выбор оси)
Подтвердите предварительный выбор оси X нажатием кнопки ОК. Откроется диалоговое окно X-Scale Axis (Ось X) (рис. 16.12). 
Рис. 16.12: Диалоговое окно X-Scale Axis (Ось X)
В редактируемом поле Displayed (Отображаемый) в рубрике Range (Диапазон) измените минимальное значение на 0. Подтвердите нажатием на ОК. Выберите вновь в меню редактора диаграмм опции Chart... (Диаграмма* Axis... (Оси) Активируйте в диалоговом окне Axis Selection (Выбор оси) опцию Y Scale (Ось Y). Откроется диалоговое окно Y-Scale Axis (Ось Y). И здесь в рубрике Range (Диапазон) в редактируемом поле Displayed (Отображаемый) измените минимальное значение на "0". Подтвердите нажатием на ОК.
В окне просмотра Вы увидите откорректированную диаграмму рассеяния (см. рис. 16.13).
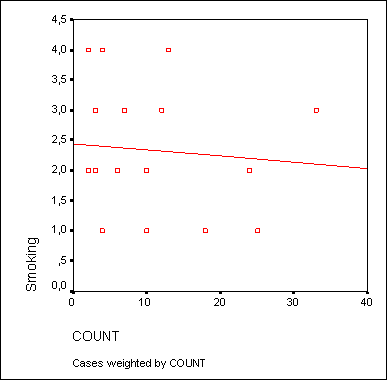
Рис. 16.13: Диаграмма рассеяния с регрессионной прямой после корректировки осей
На откорректированной диаграмме рассеяния теперь стало проще распознать начальную точку на оси Y, которая образуется при пересечении с регрессионной прямой. Значение этой точки примерно равно 2,9. Сравним это значение с уравнением регрессии для переменных puls (зависимая переменная) и konsum (независимая переменная). В результате расчёта уравнения регрессии в окне отображения результатов появятся следующие значения:
Coefficients (Коэффициенты)а
| Model (Модель) |
|
Unstandardized Coefficients
(Не стандартизированные коэффициенты) |
Standardized Coefficients (Стандартизированные коэффициенты) |
t |
Sig. (Значимость) |
| B |
Std: Error
(Станд. ошибка) |
ß (Beta) |
| 1 |
(Constant) (Константа) |
2,871 |
,639 |
|
4,492 |
,002 |
| tgl. Zigarettenkonsum |
,145 |
,038 |
,804 |
3,829 |
,005 |
a. Dependent Variable: Pulsfrequenz unter 80 (Зависимая переменная: частота пульса ниже 80)
Что дает следующее уравнение регрессии:
puls = 0,145 • konsum + 2,871
Константа в вышеприведенном уравнении регрессии (2,871) соответствует точке на оси Y, которая образуется в точке пересечения с регрессионной прямой.
|