16.2 Множественная линейная регрессия
В общем случае в регрессионный анализ вовлекаются несколько независимых переменных. Это, конечно же, наносит ущерб наглядности получаемых результатов, так как подобные множественные связи
в конце концов становится невозможно представить графически.
В случае множественного регрессионного анализа речь идёт необходимо оценить коэффициенты уравнения
у = b1 • х1 + b2 • х2+ ... + bn • хn + а,
где n — количество независимых переменных, обозначенных как х1 и хn, а — некоторая константа.
Переменные, объявленные независимыми, могут сами коррелировать между собой; этот факт необходимо обязательно учитывать при определении коэффициентов уравнения регрессии для того,
чтобы избежать ложных корреляций.
В качестве примера рассмотрим стоматологическое обследование 1130 человек, в котором исследуется вопрос необходимости лечения зубного ряда, измеряемой при помощи так называемого показателя CPITN,
в зависимости от набора различных переменных.
При этом зубной ряд был разделён на секстанты, для которых и происходило определение показателя CPITN. Этот показатель может принимать значения от 0 до 4, где 0 соответствует здоровому состоянию,
а 4 наибольшей степени развития заболевания. Затем значения показателя CPITN для всех секстант были усреднены.
Файл zahn.sav содержит следующие переменные:
| Имя переменной |
Расшифровка |
| cpitn |
Усредненное значение CPITN |
| alter |
Возраст |
| g |
Пол (1 = мужской, 2 = женский) |
| s |
Образование (1 = специальное школьное, 2 = неполное школьное, 3 = среднее, 4 = аттестат зрелости, 5 = высшее образование) |
| pu |
Периодичность чистки зубов (1 = меньше одного раза в день, 2 = один раз в день, 3 = два раза в день, 4 = долее двух раз в день) |
| zb |
Смена зубной щётки
(1 = каждый месяц, 2 = каждые три месяца, 3 = раз в полгода, 4 = ещё реже) |
| beruf |
Профессия (1 = государственный служащий/служащий, 2 = рабочий / профессиональный рабочий, 3 = занятость в области медицины, 4 = военный) |
Переменные cpitn и alter принадлежат к интервальной шкале, а переменные s, pu и zb при более подробном рассмотрении можно отнести к порядковой (ранговой) шкале,
так что они могут быть подвергнуты регрессионному анализу. Переменная g относится к номинальной шкале, но в то же время является дихотомической. Поэтому если при оценке результатов
обратить внимание на полярность, то и эта переменная так же может быть вовлечена в регрессионный анализ. Однако, переменная beruf относится к номинальной шкале и имеет более двух
(а именно четыре) категории. Поэтому, без дополнительной обработки ее нельзя применять в дальнейших расчётах.
В данном случае можно прибегнуть к специальному трюку: разложить переменную beruf на четыре, так называемых, фиктивных переменных, с кодировками отвечающими 0 (действительно) и 1 (ложно).
В файл добавляются четыре новые переменные: beruf1 - beruf4, которые поочередно соответствуют четырём различным кодировкам переменной beruf. Так, к примеру,
переменная beruf1 указывает на то, является ли данный респондент государственным служащим/работником (кодировка 1) или нет (кодировка 0).
Откройте файл zahn.sav. Выберите в меню Analyze... (Анализ) ► Regression...(Регрессия) ► Linear... (Линейная) Поместите переменную cpitn в поле для зависимых переменных, объявите переменные: alter, beraf1, bеruf2, beruf3, beruf4, g, pu, s и zb независимыми.
Для множественного анализа с несколькими независимыми переменными не рекомендуется оставлять метод включения всех переменных (Enter), установленный по умолчанию.
Этот метод соответствует одновременной обработке всех независимых переменных, выбранных для анализа, и поэтому он может рекомендоваться для использования только в случае простого
анализа с одной независимой переменной. Для множественного анализа следует выбрать один из пошаговых методов.
В списке Method имеются следующие возможности:
- Enter - простейший способ - все данные формируются в единую группу.
- Remove - это метод, который позволяет отбрасывать переменные в процессе определения конечной модели.
- Stepwise - это метод, который позволяет добавлять и удалять отдельные переменные в соответствии с параметрами, установленными в окне Options.
- Backward - данный метод позволяет последовательно удалять переменные из модели в соответствии с параметрами в окне Options, до того момента, пока это возможно (например по критерию значимости).
- Forward - данный метод позволяет последовательно добавлять переменные в модель в соответствии с параметрами в окне Options, до того момента, пока это возможно.
При прямом методе независимые переменные,
которые имеют наибольшие коэффициенты частичной корреляции с зависимой переменной пошагово увязываются в регрессионное уравнение. При обратном методе начинают с результата,
содержащего все независимые переменные и затем исключают независимые переменные с наименьшими частичными корреляционными коэффициентами, пока соответствующий регрессионный коэффициент
не оказывается незначимым (в данном случае уровень значимости равен 0,1).
Наиболее распространенным является пошаговый метод, который устроен так же, как и прямой метод, однако после каждого шага переменные, используемые в данный момент, исследуются по обратному методу.
При пошаговом методе могут задаваться блоки независимых переменных; в этом случае заданные блоки на одном шаге обрабатываются совместно.
Model Summary (Сводная таблица модели)
| Model (Модель) |
R |
R Square (Коэффициент детерминации) |
Adjusted R Square (Скорректированный R-квадрат) |
Std. Error of the Estimate (Стандартная ошибка оценки) |
| 1 |
,452а |
,204 |
,203 |
,8316 |
| 2 |
,564b |
,318 |
,317 |
,7698 |
| 3 |
,599с |
,359 |
,358 |
,7467 |
| 4 |
,609d |
,371 |
,369 |
,7402 |
| 5 |
,613е |
,375 |
,373 |
,7380 |
a. Predictors: (Constant), Alter (Влияющие переменные: (константа), возраст).
b. Predictors: (Constant), Alter, Putzhaeufigkeit (Влияющие переменные: (константа), возраст, периодичность чистки).
c. Predictors: (Constant), Alter, Putzhaeufigkeit, Zahnbuerstenwechsel (Влияющие переменные: (константа), возраст, периодичность чистки, смена зубной щётки).
d. Predictors: (Constant), Alter, Putzhaeufigkeit, Zahnbuerstenwechsel, Schulbildung (Влияющие переменные: (константа), возраст, периодичность чистки, смена зубной щётки, образование).
е. Predictors: (Constant), Alter, Putzhaeufigkeit, Zahnbuerstenwechsel, Schulbildung, Arbeiter/Facharbeiter (Влияющие переменные: (константа), возраст, периодичность чистки, смена зубной щётки, образование, рабочий/профессиональный работник).
Из первой таблице следует, что вовлечение переменных в расчет производилось за пять шагов, то есть переменные: возраст, периодичность чистки, смена зубной щётки, образование,
рабочий/профессиональный работник поочерёдно внедрялись в уравнение регрессии. Для каждого шага происходит вывод коэффициентов множественной регрессии, меры определённости,
смещенной меры определённости и стандартной ошибки.
К указанным результатам пошагово присоединяются результаты расчёта дисперсии, которые здесь не приводятся. Также, пошаговым образом, производится вывод соответствующих коэффициентов регрессии
и значимость их отличия от нуля.
Coefficients (Коэффициенты)a
| Model (Модель) |
|
Unstandardized Coefficients
(Не стандартизированные коэффициенты) |
Standardized Coefficients (Стандартизированные коэффициенты) |
t |
Sig. (Значимость) |
| B |
Std: Error
(Станд. ошибка) |
ß (Beta) |
| 1 |
(Constant)
Возраст |
1,295
,0331 |
,071
,002 |
,452 |
18,220
17,006 |
,000
,000 |
| 2 |
(Constant)
Возраст
Периодичность чистки |
3,024
,032
-,604 |
,142
,002
,044 |
,437
-,339 |
21,317
17,765
-13,756 |
,000
,000
,000 |
| 3 |
(Constant)
Возраст
Периодичность чистки
Смена зубной щётки |
1,903
,0325
-,439
,253 |
,191
,002
,047
,030 |
,443
-,246
,222 |
9,976
18,555
-9,376
8,473 |
,000
,000
,000
,000 |
| 4 |
(Constant)
Возраст
Периодичность чистки
Смена зубной щётки
Образование |
2,188
,0331
-,391
,226
-,115 |
,199
,002
,048
,030
,025 |
,451
-,220
,199
-,116 |
10,992
19,011
-8,235
7,498
-4,580 |
,000
,000
,000
,000
,000 |
| 5 |
(Constant)
Возраст
Периодичность чистки
Смена зубной щётки
Образование
Рабочий |
2,022
,032
-,379
,229
-,083
,143 |
,208
,002
,048
,030
,028
,052 |
,437
-,213
,201
-,084
,075 |
9,743
18,041
-7,964
7,613
-2,983
2,757 |
,000
,000
,000
,000
,003
,006 |
а. Dереnаdеnt variable: Mittlerer CPITN-Wert (Зависимая переменная: усреднённое значение CPITN)
Вдобавок ко всему для каждого шага анализируются исключённые переменные. В вышеприведенной таблице в объяснениях нуждаются лишь коэффициенты ß. Это — регрессионные коэффициенты,
стандартизованные соответствующей области значений, они указывают на важность независимых переменных, вовлечённых в регрессионное уравнение.
Уравнение регрессии для прогнозирования значения CPITN выглядит следующим образом:
cpitn = 0,032 • alter - 0.379 • рu + 0,229 • zb - 0,083 • s + 0,143 • benuf2 + 2,022
Для 40-летнего рабочего с неполным школьным образованием, который ежедневно чистит зубы один раз в день и меняет щётку раз в полгода, с учётом соответствующих кодировок, получается следующее уравнение:
cpitn = 0,032 • 40 - 0,379 • 2 + 0,229 • 3 - 0,083 • 2 + 0,143 • 1 + 2,022 = 3,208
При помощи соответствующих опций можно организовать вывод большого числа дополнительных статистических характеристик и графиков, на которых мы здесь останавливаться не будем.
Можно также создать много дополнительных переменных и добавить их в исходный файл данных.
Коллинеарность
Важным шагом перед запуском процедуры построения регрессионной модели может быть пункт Collinearity Diagnostics в диалоговом окне Statistics....
Установление требования провести диагностику наличия коллинеарности между независимыми переменными позволяет избежать эффекта мультиколлинеарности, при котором несколько независимых переменных
могут иметь настолько сильную корреляцию, что в регрессионной модели обозначают, в принципе, одно и то же (это неприемлемо).
Результат диагностики коллинеарности показан в таблице Coefficients в колонках Collinearity Statistics.
Если величина значения VIF (Variance Inflation Factor) возле каждой независимой переменной меньше 10 — значит, эффекта мультиколлинеарности не наблюдается и регрессионная модель приемлема для дальнейшей интерпретации.
Чем выше показатель VIF, тем более связаны между собой переменные. Если какая-либо переменная превышает значение в 10 VIF, следует пересчитать регрессию без этой независимой переменной.
Анализ остатков
Важным моментом является анализ остатков, то есть отклонений наблюдаемых значений от теоретически ожидаемых. Остатки должны появляться случайно (то есть не систематически)
и подчиняться нормальному распределению. Это можно проверить, если с помощью кнопки Charts... (Диаграммы) построить гистограмму остатков. В приведенном примере наблюдается довольно хорошее
согласование гистограммы остатков с нормальным распределением.
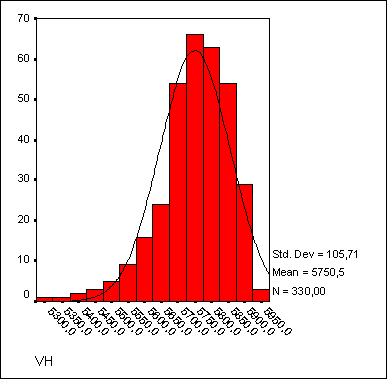
Рис. 16.14: Гистограмма остатков
Автокорреляция остатков модели регрессии
Проверка на наличие систематических связей между остатками соседних случаев,
может быть произведена при помощи теста Дарбина-Ватсона (Durbin-Watson) на автокорреляцию остатков.
Остатки должны быть случайными, однако при моделировании нередко встречается ситуация, когда остатки содержат тенденцию или циклические колебания.
Это свидетельствует о том, что каждое следующее значение остатков зависит от предшествующих. В этом случае говорят об автокорреляции остатков модели регрессии.
Автокорреляция в остатках может быть вызвана несколькими причинами, имеющими различную природу.
Иногда причину автокорреляции остатков следует искать в формулировке модели. В модель может быть не включен фактор, оказывающий существенное воздействие на результат,
но влияние которого отражается в остатках, вследствие чего последние могут оказаться автокоррелированными. Зачастую этим фактором является фактор времени t.
Либо модель не учитывает несколько второстепенных факторов, совместное влияние которых на результат существенно ввиду совпадения тенденций их изменения или фаз циклических колебаний.
Тест Дарбина-Ватсона вычисляет коэффициент, лежащий в диапазоне от 0 до 4. Если значение этого коэффициента находится вблизи 2, то это означает, что автокорреляция отсутствует.
Этот тест можно активировать через кнопку Statistics (Статистические характеристики). В данном примере тест дает удовлетворительное значение коэффициента, равное 1,776.
Ещё одной дополнительной возможностью является задание переменной отбора в диалоговом окне Linear Regression (Линейная регрессия). Здесь, с помощью кнопки Rule... (Правило) в диалоговом окне
Linear Regression: Define Selection Rule (Линейная регрессия: ввод условия отбора), Вы получаете возможность при помощи избирательного признака сформулировать условие,
которое будет ограничивать количество случаев, вовлеченных в анализ.
|