16.5. Мультиномиальная логистическая регрессия
Этот метод является вариантом логистической регрессии, при которой зависимая переменная не является дихотомической, как при бинарной логистической регрессии, а имеет больше двух категорий.
В то время как, при бинарной логистической регрессии независимая переменная может иметь интервальную шкалу, то мультиномиальная логистическая регрессия пригодна только для
категориальных независимых переменных, причём имеет значение, относятся ли они к шкале наименований или к порядковой шкале. Конечно же, не исключается возможность задания в
качестве ковариат переменных, имеющих интервальную шкалу.
Для независимых переменных, относящихся к порядковой шкале предусмотрен метод порядковой регрессии,
который в данном случае является предпочтительным.
Для представления метода мультиномиальной логистической регрессии был сначала взят простой пример с одной независимой переменной. Данные для этого примера были взяты из ALLBUS
(общий социологический опрос населения) 1998 года.
Частотные таблицы для четырёх переменных, находящихся в этом файле, выглядят так:
Alter (Возраст)
|
Frequency (Частота) |
Percent (Процент) |
Valid Percent (Действительный процент) |
Cumulative Percent (Совокупный процент) |
| Valid (Действительное значение) |
Bis 45 Jahre
(До 45 лет) |
1306 |
50,1 |
50,1 |
50,1 |
Über 45 Jahre
(Свыше 45 лет) |
1301 |
49,9 |
49,9 |
100,0 |
| Total (Сумма) |
2607 |
100,0 |
100,0 |
|
Politische Links-Rechts-Einschaetzung (Политическая принадлежность к левым или правым)
|
Frequency (Частота) |
Percent (Процент) |
Valid Percent (Действительный процент) |
Cumulative Percent (Совокупный процент) |
| Valid (Действительное значение) |
Eher links
(Скорее левый) |
740 |
28,4 |
28,4 |
28,4 |
Mitte
(Центрист) |
1212 |
46,5 |
46,5 |
74,9 |
eher rechts
(Скорее правый) |
655 |
25,1 |
25,1 |
100,0 |
| Total (Сумма) |
2607 |
100,0 |
100,0 |
|
Schicht (Прослойка)
|
Frequency (Частота) |
Percent (Процент) |
Valid Percent (Действительный процент) |
Cumulative Percent (Совокупный процент) |
| Valid (Действительное значение) |
Unterschicht
(Нижняя прослойка) |
879 |
33,7 |
33,7 |
33,7 |
Mittelschicht
(Средняя прослойка) |
1477 |
56,7 |
56,7 |
90,4 |
Oberschicht
(Верхняя прослойка) |
251 |
9,6 |
9,6 |
100,0 |
| Total (Сумма) |
2607 |
100,0 |
100,0 |
|
Schulbildung (Школьное образование)
|
Frequency (Частота) |
Percent (Процент) |
Valid Percent (Действительный процент) |
Cumulative Percent (Совокупный процент) |
| Valid (Действительное значение) |
Hauptschule (Неполное среднее) |
1499 |
57,5 |
57,5 |
57,5 |
| Mittlere Reife (Среднее) |
610 |
23,4 |
23,4 |
80,9 |
| Abitur (Атестат зрелости) |
498 |
19,1 |
19,1 |
100,0 |
| Total (Сумма) |
2607 |
100,0 |
100,0 |
|
Мы хотим рассмотреть переменную polire (Политическая принадлежность к левым или правым) как зависимую переменную, а три остальные — как независимые переменные (факторы).
В первом примере в качестве независимой переменной мы возьмем только переменную Alter (Возраст). Прежде всего построим таблицу сопряженности для этих двух переменных.
Переменной alter присвойте статус строчной переменной (Row(s)), a polire — столбцовой переменной (Column(s)),
и через выключатель Cells... (Ячейки) активируйте вывод процентных показателей для ячеек.
Alter * Politische Links-Rechts-Einschfltzung Crosstabulation
(Возраст * Политическая принадлежность к левым или правым - таблица сопряженности)
|
Politische Links-Rechts-Einschfltzung
(Политическая принадлежность) |
Total (Сумма) |
Eher links
(Скорее левый) |
Mitte
(Центрист) |
Eher rechts
(Скорее правый) |
| Alter (Возраст) |
Bis 45 Jahre
(До 45 лет) |
Count
(Количество) |
446 |
615 |
245 |
1306 |
% within Alter
(% от возраста) |
34,2% |
47,1% |
18,8% |
100,0% |
Über 45 Jahre
(Свыше 45 лет) |
Count % of Total
(Количество) |
294 |
597 |
410 |
1301 |
% within Alter
(% от возраста) |
22,6% |
45,9% |
31,5% |
100,0% |
Total
(Сумма) |
|
Count
(Количество) |
740 |
1212 |
655 |
2607 |
% within Alter
(% от возраста) |
28,4% |
46,5% |
25,1% |
100,0% |
Для младшей возрастной категории политическое самоопределение имеет тенденцию склонения симпатий к левым партиям, а для старшей — скорее к правым.
Рассмотрим простую мультиномиальную логистическую модель, которая отражает взаимосвязь между политическим самоопределением и возрастом.
Так как политическое самоопределение, как зависимая переменная, включает три категории, то для определения вероятностей отнесения респондентов к этим трем категориям можно сформировать
два недублированных логита, причём последняя категория "eher rechts" (скорее правый) будет использоваться как эталонная:
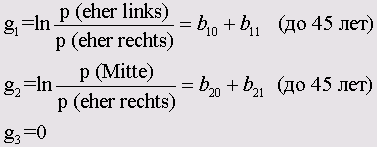
Нахождение коэффициентов b10, b11, b20 и b21 (называемых параметрическими оценками) и является основной задачей мультиномиальной логистической регрессии.
Первая цифра индекса указывает на номер логита, а вторая на порядковый номер коэффициента в данном логите, причём цифра 0 на второй позиции индекса означает константу,
за которой далее следует ровно столько коэффициентов, сколько независимых переменных (факторов) взято в рассмотрение. Коэффициентам последней (эталонной) категории присваивается значение 0.
Переменная Alter (Возраст), как единственная независимая переменная, имеет две категории, одна из которых рассматривается как эталонная, ее коэффициенты принимаются равными 0.
Выберите в меню Analyze (Анализ) ► Regression ...(Регрессия) ► Multinomial Logistic... (Мультиномиальная логистическая). Откроется диалоговое окно Multinomial Logistic Regression (Мультиномиальная логистическая регрессия). 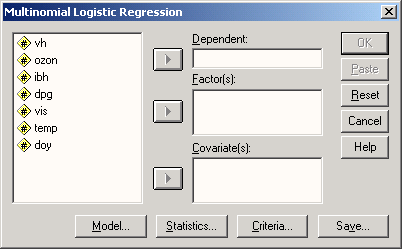
Рис. 16.17: Диалоговое окно Multinomial Logistic Regression (Множественная логистическая регрессия)
Переменную polire поместите в поле для зависимых переменных, а переменную alter (возраст) в поле для факторов. Нажмите выключатель Statistics (Статистики). Откроется диалоговое окно Multinomial Logistic Regression: Statistics (Мультиномиальная логистическая регрессия: Статистики) 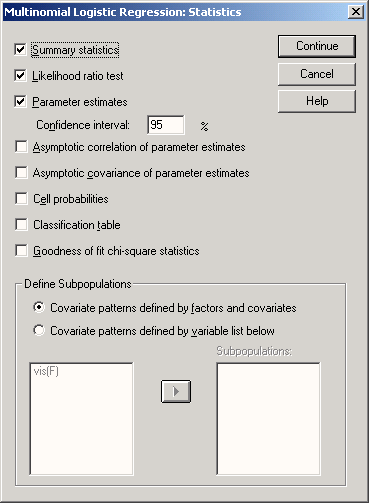
Рис. 16.18: Диалоговое окно Multinomial Logistic Regression: Statistics (Множественная логистическая регрессия: Статистики)
Оставьте активированным вывод параметрических оценок с доверительным интервалом соответствующим 95 % и покиньте это диалоговое окно нажатием Далее и ОК.
Содержание таблицы результатов расчёта, выглядит следующим образом. Для не дублирующих категорий она содержит параметрические оценки, стандартную ошибку, проверку значимости при помощи статистики Вальда,
значение экспоненциальной функции от параметрической оценки и его доверительный интервал.
Parameter Estimates (Оценки параметров)
| Politische Links-Rechts-Einschaetzung (Политическая принадлежность к левым или правым) |
В |
Std. Error (Стандартная ошибка) |
Wald (Вальд) |
df (Степень свободы) |
Sig. (Значимость) |
Ехр(В) |
95% Confidence Interval for Ехр(В) (95% доверительный интервал для Ехр(В)) |
| Lower Bound (Нижний предел) |
Upper Bound (Верхний предел) |
| eher links (Скорее левый) |
Intercept (Постоянное слагаемое) |
-,333 |
,076 |
18,938 |
1 |
,000 |
|
|
|
| [alter = 1,00] |
,932 |
,110 |
71,353 |
1 |
,000 |
2,539 |
2,045 |
3,151 |
| [alter = 2,00] |
0b |
. |
. |
0 |
. |
. |
. |
. |
| Mitte (Центрист) |
Intercept (Постоянное слагаемое) |
,376 |
,064 |
34,320 |
1 |
,000 |
|
|
|
| [alter = 1,00] |
,545 |
,099 |
30,198 |
1 |
,000 |
1,724 |
1,420 |
2,094 |
| [alter = 2,00] |
0b |
. |
. |
. |
. |
. |
. |
. |
a. This parameter is set to zero because it is redundant (Данный параметр обнуляется, т.к. он является дублирующим)
Из таблицы можно взять следующие значения для b-коэффициентов:
b10 = -0,333
b11 (до 45 лет) = 0,932
b20 = 0,376
b21 (до 45 лет) = 0,545
Таким образом, для возрастной группы до 45 лет получим:
g1 = -0,333 + 0,932 = 0,599
g2 = -0,376 + 0,545 = 0,921
и следовательно
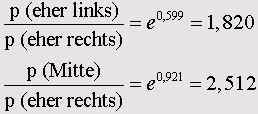
Для дублирующего логита по правилам вычисления логарифма справедливо
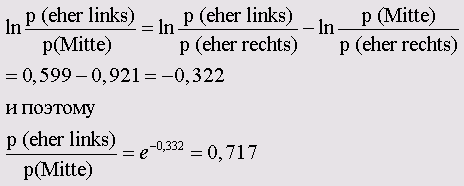
К примеру, в возрастной категории до 45 лет вероятность быть более склонным к левым течениям в 1,820 раз выше вероятности склонности к правым течениям.
Такой же расчёт можно произвести и для другой возрастной категории; в данном случае будут отсутствовать коэффициенты
b11 и b21, т.к. они приравниваются к нулю.
Следует отметить, что прямое определение вероятности для трёх категорий политической самооценки, интересней, чем соотношение этих вероятностей между собой.
Для каждой i-ой категории зависимых переменных эта вероятность может быть вычислена по следующей формуле:
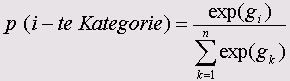
Здесь для большей удобочитаемости экспоненциальная функция обозначена как ехр. n указывает на число категорий (здесь n=3).
Для возрастной группы до 45 лет для трёх категорий политической самооценки получатся следующие вероятности:
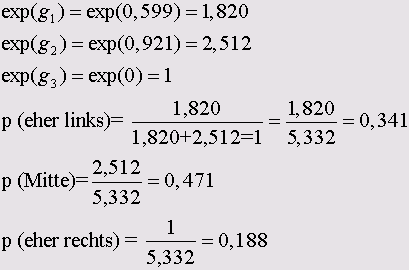
Стало быть, для отдельного человека, принадлежащего к возрастной группе до 45 лет вероятность склонения политической самооценки в сторону левых составляет, 0,341 или 34,1%, в сторону центристов 47,1%
и в сторону правых 18,8%. Эти числа соответствуют процентным показателям таблицы сопряженности для возраста и политической самооценки. Таким образом, в случае наличия лишь одной независимой
переменной легко удостовериться в правдоподобности расчётов, производимых при мультиномиальной логистической регрессии.
Для возрастной группы свыше 45 лет расчёты будут выглядеть следующим образом:
g1 = -0,333 + 0 = -0,333
g2 = 0,376 + 0 = 0,376
g3= 0
ехр (g1) = ехр (-0,333) = 0,717
ехр (g2) = ехр (0,376) = 1,456
ехр (g3) = ехр (0) = 1
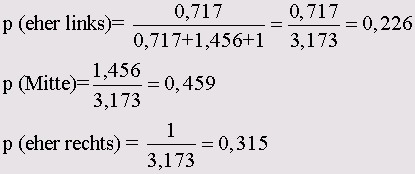
Если выразить полученные показатели в процентах, то и здесь так же наблюдается полное согласование с соответствующими процентными показателями таблицы сопряженности.
Следует отметить, что только в случае наличия лишь одной независимой переменной, как в приведённом примере, проведение расчёта с применением столь громоздкого метода,
как многозначная логистическая регрессия, является достаточно бессмысленным — все соотношения могут быть выяснены проще, при помощи таблиц сопряженности.
Поэтому мы введем в рассмотрение ещё одну дополнительную переменную — переменную schule (образование).
В диалоговом окне Multinomial Logistic Regression (Мультиномиальная логистическая регрессия) поместите переменную schule вместе с переменной alter в поле факторов. В диалоговом окне Multinomial Logistic Regression: Statistics (Мультиномиальная логистическая регрессия: Статистики) активируйте дополнительные опции Cell probabilities (Вероятность по ячейкам)
и Likelihood ratio test (Тест отношения правдоподобия) и начните расчёт вновь.
Таблица теста коэффициентов правдоподобия содержит изменения функции правдоподобия для случая, когда исключается соответствующий главный действующий фактор;
эти изменения выражаются через соответствующие значения теста X2 (хи-квадрат). Выдаваемый уровень значимости р < 0,001 указывает на то, что оба фактора (возраст и школьное образование)
оказывают очень значимое влияние на зависимую переменную (политическая самооценка).
Model Fitting Information (Информация о приближении, обеспечиваемой моделью)
| Model (Модель) |
-2 Log likelihood
(-2 логарифмическое правдоподобие) |
Chi-square (Хи-квадрат) |
df (степень свободы) |
Sig. (Значимость) |
| Intercept Only (Только постоянное слагаемое) |
252,208 |
|
|
|
| Final (Окончательно) |
93,429 |
158,779 |
6 |
,000 |
Likelihood Ratio Tests (Тест отношения правдоподобия)
| (Результат) |
-2 Log Likelihood of Reduced Model
(-2 логарифмическое правдоподобие для сокращённой модели) |
Chi-square (Хи-квадрат) |
df
(Степень свободы) |
Sig. (Значимость) |
Intercept
(Постоянное слагаемое) |
93,429 |
,000 |
0 |
|
| ALTER (Возраст) |
171,496 |
78,067 |
2 |
,000 |
| SCHULE (Образование) |
178,489 |
85,060 |
4 |
,000 |
The chi-square statistic is the difference in -2 log-likelihoods between the final model and a reduced model. The reduced model is formed by omitting an effect from the final model.
The null hypothesis is that all parameters of that effect are 0 (Статистика хи-квадрат отображает различие -2 логарифмического правдоподобия между окончательной моделью и усеченной моделью.
Суть расчёта усеченной модели сводится к тому, что из окончательной модели исключается один фактор влияния.
Нулевая гипотеза соответствует обнулению всех параметров параметрических оценок данного фактора влияния).
Таблица (b — коэффициентов) выглядит следующим образом.
Parameter Estimates (Оценки параметров)
| Politische Links-Rechts-Einschaetzung (Политическая принадлежность к левым пли правым) |
В |
Std. Error (Стандартная ошибка) |
Wald (Вальд) |
df (Степень свободы) |
Sig. (Значимость) |
Exp (В) |
95% Confidence Interval for Exp(B) (95% доверительный интервал для Ехр(В)) |
| Lower Bound (Нижний предел) |
Upper Bound (Верхний предел) |
| eher links (Скорее левый) |
(Постоянное слагаемое) |
-,129 |
,137 |
,890 |
1 |
,345 |
|
|
|
| [alter = 1,00] |
,952 |
,117 |
66,600 |
1 |
,000 |
2,591 |
2,061 |
3,256 |
| [alter = 2,00] |
0a |
0 |
, |
0 |
, |
, |
, |
, |
| [schule = 1,00] |
-,179 |
,142 |
,592 |
1 |
,207 |
,836 |
,632 |
1,104 |
| [schule = 2,00] |
-,480 |
,158 |
9,249 |
1 |
,002 |
,619 |
,454 |
,843 |
| [schule = 3,00] |
0b |
0 |
, |
0 |
, |
, |
, |
, |
| Mine (Центрист) |
(Постоянное слагаемое) |
-,236 |
,137 |
2,982 |
1 |
,084 |
|
|
|
| [alter = 1,00] |
,766 |
,106 |
52,174 |
1 |
,000 |
2,152 |
1,748 |
2,939 |
| [alter = 2,00] |
Ob |
0 |
, |
0 |
, |
, |
, |
, |
| [schule = 1,00] |
,802 |
,141 |
32,539 |
1 |
,000 |
2,231 |
1,693 |
2,939 |
| [schule = 2,00] |
,149 |
,155 |
,922 |
1 |
,337 |
1,161 |
,856 |
1,574 |
| [schule = 3,00] |
Ob |
0 |
, |
0 |
, |
, |
, |
, |
a. This parameter is set to zero because it is redundant (Данный параметр обнуляется, так как он является дублирующим)
В качестве примера определим вероятности для политической самооценки отдельного человека, принадлежащего к возрастной группе свыше 45 лет с неполным средним образованием.
Для этого по аналогии с предыдущим примером произведём следующие вычисления:
g1 = -0,129 + 0 - 0,179 = -0,308
g2 = -0,236 + 0 + 0,802 = 0,566
g3 = 0
exp (g1) = 0,735
exp (g2) = 1,761
exp (g3) = 1
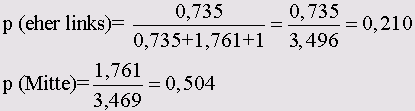
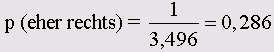
Если перевести данные результаты в процентные показатели, то они будут означать, что среди граждан в возрасте свыше 45 лет с неполным средним образованием 21,0%
симпатизируют левым политическим течениям, 28,6% правым, а 50,4% остаются по центру.
Нет необходимости вычислять процентные показатели вероятностей самостоятельно. Вы можете взять их из следующей таблицы, отображающей наблюдаемые и прогнозируемые частоты:
Observed and Predicted Frequencies (Наблюдаемые и прогнозируемые частоты)
| Schulbildung (Образование) |
Alter (Возраст) |
Politische Links-Rechts-Einschfltzung (Политическая принадлежность) |
Frequency (Частота) |
Percentage (Процент) |
| Observed (Наблюдаемая) |
Predicted (Прогнозируемая) |
Pearson Residual (Остаток Пирсона) |
Observed (Наблюдаемый) |
Predicted (Прогнозируемый) |
| Hauptschule (Неполное среднее) |
bis 45 Jahre (До 45 лет) |
eher links (Скорее левый) |
143 |
157,488 |
-1,365 |
25,8% |
28,4% |
| Mitte (Центрист) |
312 |
313,760 |
-,151 |
56,3% |
56,6% |
| eher rechts (Скорее правый) |
99 |
82,752 |
1,937 |
17,9% |
14,9% |
| über 45 Jahre (Свыше 45 лет) |
eher links (Скорее левый) |
213 |
198,512 |
1,157 |
22,5% |
21,0% |
| Mitte (Центрист) |
478 |
476,240 |
,115 |
50,6% |
50,4% |
| eher rechts (Скорее правый) |
254 |
270,248 |
-1,170 |
26,9% |
28,6% |
| Mifflere Reife (Среднее) |
bis 45 Jahre (до 45 лет) |
eher links (Скорее левый) |
129 |
131,561 |
-,271 |
31,5% |
32,2% |
| Mitte (Центрист) |
192 |
184,113 |
,784 |
46,9% |
45,0% |
| eher rechts (Скорее правый) |
88 |
99,326 |
-,628 |
21,5% |
22.8% |
| über 45 Jahre(Свыше 45 лет) |
eher links (Скорее левый) |
47 |
44,439 |
,435 |
23,4% |
22.1% |
| Mitte (Центрист) |
67 |
74,887 |
-1,151 |
33,3% |
37,3% |
| eher rechts (Скорее правый) |
87 |
81,674 |
,765 |
43,3% |
40,6% |
| Abitur (Аттестат зрелости) |
bis 45 Jahre (до 45 лет) |
eher links (Скорее левый) |
174 |
156,952 |
1,848 |
50,7% |
45,8% |
| Mitte (Центрист) |
111 |
117,127 |
-,698 |
32,4% |
34,1% |
| eher rechts (Скорее правый) |
58 |
68,922 |
-1,472 |
16,9% |
20,1% |
| über 45 Jahre (Свыше 45 лет) |
eher links (Скорее левый) |
34 |
51,048 |
-2,914 |
21,9% |
32,9% |
| Mitte (Центрист) |
52 |
45,873 |
1,078 |
33,5% |
29,6% |
| eher rechts (Скорее правый) |
69 |
58,078 |
1,812 |
44,5% |
37,5% |
The percentages are based on total observed frequencies in each subpopulation (Процентные показатели основываются на наблюдаемых суммарных частотах для каждой частичной совокупности).
Теперь вы можете видеть, что наблюдаемые и прогнозированные значения оказались рассогласованными. Это произошло потому, что теперь в модель входят только главные факторы влияния, а не взаимодействия.
Откроется диалоговое окно Multinomial Logistic Regression: Model (Мультиномиальная логистическая регрессия: Модель).
Вы можете включить в расчёт все главные факторы влияния и взаимодействия, если вместо предварительно установленной по умолчанию опции Main effects (Основные эффекты) активируете опцию Full factorial
(Полнофакторная модель). При помощи опции Custom (Пользовательский режим), Вы можете отобрать включаемые в расчёт факторы влияния.
В таблице оценки параметра теперь находятся и взаимодействия. Если Вы обратите внимание на наблюдаемые и ожидаемые частоты, то заметите, что теперь они совпадают.
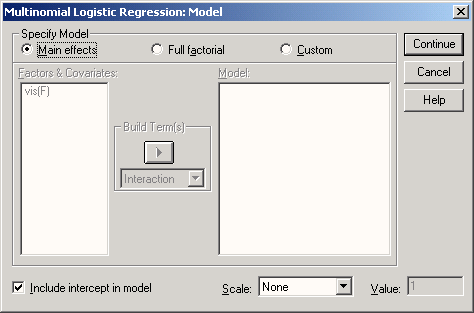
Рис. 16.19: Диалоговое окно Multinomial Logistic Regression: Model (Множественная логистическая регрессия: Модель)
|