16.6. Порядковая регрессия
В то время как, мультиномиальная регрессия предназначена для зависимой переменной, относящейся к номинальной шкале,
то порядковая регрессия предназначена для целевой переменной, принадлежащей к порядковой шкале. Независимые переменные и здесь должны быть категориальными
(то есть иметь номинальную или порядковую шкалу), однако в качестве ковариат допускается применение переменных с интервальной шкалой.
Изучим данный метод при помощи примера из области психологии. Будет рассматриваться "Анкета о специфике лечения психических заболеваний в больнице Фрайбурга",
которая дает представление о работе с пациентами на основании 35 отдельных пунктов. К примеру, восприимчивость пациента к целенаправленным лечебным действиям выясняется при помощи пункта
"Разработать план и затем приступить к его воплощению", причём ответ даётся в соответствии с пятибалльной шкалой: от "абсолютно не верно" (кодировка 1) до "абсолютно верно" (кодировка 5).
Эта типичная порядковая переменная должна быть исследована в зависимости от возраста, пола, продолжительности болезни и образования. Значения приведенных переменных были собраны в отношении
85 пациентов и находятся в файле plan.sav.
Alter (Возраст)
|
Frequency (Частота) |
Percent
(Процент) |
Valid Percent (Действительный процент) |
Cumulative percent (Совокупный процент) |
| Valid (Действительное значение) |
bis 40 Jahre
(Дo 45 лет) |
29 |
34,1 |
34,1 |
34,1 |
41-55 Jahre
(41-55 лет) |
29 |
34,1 |
34,1 |
68,2 |
ueber 55 Jahre
(Свыше 55 лет) |
27 |
31,8 |
31,8 |
100,0 |
| Total (Сумма) |
85 |
100,0 |
100,0 |
|
Geschlecht (Пол)
|
Frequency (Частота) |
Percent
(Процент) |
Valid Percent (Действительный процент) |
Cumulative percent (Совокупный процент) |
| Valid (Действительное значение) |
Maennlich (Мужской) |
44 |
51,8 |
51,8 |
51,8 |
| Weiblich (Женский) |
41 |
48,2 |
48,2 |
100,0 |
| Total (Сумма) |
85 |
100,0 |
100,0 |
|
Krankheitsdauer (Продолжительность болезни)
|
Frequency (Частота) |
Percent
(Процент) |
Valid Percent (Действительный процент) |
Cumulative percent (Совокупный процент) |
| Valid (Действительное значение) |
bis 5 Jahre
(До 5 лет) |
24 |
28,2 |
28,2 |
28,2 |
6-10 Jahre
(6-1О лет) |
16 |
18,8 |
18,8 |
47,1 |
11-20 Jahre
(11-20 лет) |
32 |
37,6 |
37,6 |
84,7 |
ueber 20 Jahre
(Свыше 20 лет) |
13 |
15,3 |
15,3 |
100,0 |
| Total (Сумма) |
85 |
100,0 |
100,0 |
|
Schulbildung (Образование)
|
Frequency (Частота) |
Percent
(Процент) |
Valid Percent (Действительный процент) |
Cumulative percent (Совокупный процент) |
| Valid (Действительное значение) |
Hauptschule (непол. среднее) |
53 |
62,4 |
62,4 |
62,4 |
| Mittlere Reife (среднее) |
18 |
21,2 |
21,2 |
83,5 |
| Abitur (аттестат зрелости) |
14 |
16,5 |
16,5 |
100,0 |
| Total (Сумма) |
85 |
100,0 |
100,0 |
|
Einen Plan machen und danach handeln (Разработать план и затем приступить к его воплощению)
|
Frequency (Частота) |
Percent
(Процент) |
Valid Percent (Действительный процент) |
Cumulative percent (Совокупный процент) |
| Valid (Действительное значение) |
gar nicht
(абс. не верно) |
24 |
28,2 |
28,2 |
28,2 |
| Wenig (слабо) |
18 |
21,2 |
21,2 |
49,4 |
| mittelmaessig (посредственно) |
18 |
21,2 |
21,2 |
70,6 |
| ziemlich (достаточно) |
16 |
18,8 |
18,8 |
89,4 |
sehr stark
(абс. верно) |
9 |
10,6 |
10,6 |
100,0 |
| (Сумма) |
85 |
100,0 |
100,0 |
|
Если с помощью меню Analyze...(Анализ) ► Correlate (Корреляция) ► Bivariate... (Парная) произвести расчёт ранговой корреляции по Спирману между пунктом
"Составить план и затем приступить к его воплощению" и другими переменными, то получите следующий результат:
Correlations (Корреляции)
|
Einen Plan machen und danach handeln (Разработать план и затем приступить к его воплощению) |
| Spearman's rho (p Спирмана) |
Alter (Возраст) |
Correlation Coefficient (Корреляционный коэффициент) |
-,376** |
| Sig. (2-tailed) (Значимость (2-сторонняя)) |
,000 |
| N |
85 |
| Geschlecht (Пол) |
Correlation Coefficient (Корреляционный коэффициент) |
,298** |
| Sig. (2-tailed) (Значимость (2-сторонняя)) |
,006 |
| N |
85 |
| Krankheitsda uer (Продолжительность болезни) |
Correlation Coefficient (Корреляционный коэффициент) |
-,260* |
| Sig. (2-tailed) (Значимость (2-сторонняя)) |
,016 |
| N |
85 |
Schulbildung
(Образование) |
Correlation Coefficient (Корреляционный коэффициент) |
,314** |
| Sig. (2-tailed) (Значимость (2-сторонняя)) |
,003 |
| N |
85 |
**. Correlation is significant at the .01 level (2-tailed) (Корреляция является значимой на уровне 0,01 (2 - сторонняя)).
*. Correlation is significant at the .05 level (2-tailed) (Корреляция является значимой на уровне 0,01 (2 - сторонняя)).
Стало быть, существует значимая, хоть и не очень большая корреляция. Если учесть принятое кодирование переменных, то можно заметить, что женщины более склонны сначала составить план действий,
а затем приступать к лечению, чем мужчины. Кроме того, более молодые пациенты, пациенты с непродолжительным периодом болезни и пациенты, имеющие высшее образование,
более активно занимаются своим лечением.
Попытаемся теперь изучить одновременное влияние возраста, пола, продолжительности болезни и образования на целевую переменную "Разработать план и затем приступить к его воплощению".
Подходящим методом для этого является порядковая регрессия.
Рис. 16.20: Диалоговое окно Ordinal Regression (Порядковая регрессия)
Переменной plan (план) присвойте статус зависимой переменной, а переменным alter (возраст), g, kdauer (продолжительность болезни) и schule (образование) — статус факторов. В поле Covariate(s) (Ковариаты) вы можете внести ковариаты, относящиеся к интервальной шкале. Однако, в нашем примере таковые отсутствуют. Нажмите кнопку Options... (Опции).
Наряду с параметрами, которые управляют итерационным процессом (предварительные установки для них мы оставляем без изменения), можно выбрать одну из пяти связующих функций, смысл которых будет пояснен далее.
Функцией, установленной по умолчанию, является Logit (Логит); эта связь, как правило, оказывается лучшей.
Щёлкните на кнопке Output... (Вывод). Откроется диалоговое окно Ordinal Regression:Output (Порядковая регрессия: Вывод). Здесь Вы получаете возможность управлять данными, выводимыми в окне просмотра и создавать новые переменные. 
Рис. 16.21. Диалоговое окно Ordinal Regression: Output (Порядковая регрессия: Вывод)
В разделе Display (Показать) оставьте предварительные установки Goodness of Jit statistics (Статистика критерия согласия), Summary statistics (Отчётная статистика) и
Parameter estimates (Параметрические оценки). В разделе Saved variables (Сохранённые переменные) активируйте опции Estimated response probabilities (Оценочные вероятности отклика),
Predicted category (Прогнозируемая категория) и Predicted category probability (Вероятность прогнозируемой категории). Теперь нажмите кнопку Location... (Положение). Здесь у Вас появляется возможность выбора между моделью, которая содержит только главные факторы влияния и, в случае необходимости,
— ковариаты, а также моделью, которую Вы можете подобрать самостоятельно (Custom). В последнем случае у Вас появляется возможность учесть также все мыслимые взаимодействия.
В данном случае, сначала мы хотим учесть только главные эффекты, что соответствует предварительной установке. Посредством кнопки Scale... (Шкала) можно ввести, так называемые, компоненты шкалы. Как правило, это не является необходимым, и мы от них откажемся. Начните расчёт нажатием ОК.
Отображение результатов в окне просмотра начинается с вывода предостережения. В 66,2% всех ячеек, которые образовываются из комбинаций факторов и зависимых переменных, частота равна нулю.
При этом не учитываются те комбинации факторов, которые повторяются. Вы можете включить в список выдачи наблюдаемые и ожидаемые частоты, а также их остатки, если после нажатия кнопки Output... (Вывод)
активируете опцию Cell information (Информация по ячейкам).
Warnings (Предостережения)

Далее следует таблица, содержащая абсолютные и выраженные в процентах частоты различных категорий зависимых переменных и факторов.
Case Processing Summary (Сводная таблица обработки наблюдений)
|
N (Количество) |
Marginal Percentage (Предельный процент) |
| Einen Plan machen und danach handeln (Разработать план и затем приступать к лечению) |
gar nicht (Абсолютно не верно) |
24
|
28,2%
|
|
wenig (Слабо)
|
18
|
21,2%
|
|
mittelmaessig (Посредственно)
|
18
|
21,2%
|
|
ziemlich (Достаточно)
|
16
|
18,8%
|
|
sehr stark (Абсолютно верно)
|
9
|
10,6%
|
|
Alter (Возраст)
|
bis 40 Jahre (До 45 лет)
|
29
|
34,1%
|
|
41-55 Jahre (41-55 лет)
|
29
|
34,1%
|
|
ueber 55 Jahre (Свыше 55 лет)
|
27
|
31,8%
|
|
Geschlecht (Пол)
|
maennlich (Мужской)
|
44
|
51,8%
|
|
weiblich (Женский)
|
41
|
48,2%
|
|
Krankheitsdauer (Продолжительность болезни)
|
bis 5 Jahre (До 5 лет)
|
24
|
28,2%
|
|
6-10 Jahre (6-10 лет)
|
16
|
18,8%
|
|
(6-10 лет)
|
32
|
37,6%
|
|
11-20 Jahre (11 -20 лет)
|
13
|
15,3%
|
|
Schulbildung (Образование)
|
Hauptschule (Неполное среднее)
|
53
|
62,4%
|
|
Mittlere Reife (Среднее)
|
18
|
21,2%
|
|
Abitur (Аттестат зрелости)
|
14
|
16,5%
|
|
Valid (Действительное значение)
|
85
|
100,0%
|
|
Missing (Пропущенное значение)
|
0
|
|
|
Tola (Сумма)
|
85
|
|
В качестве оценки значимости вклада отдельных независимых переменных в улучшение прогнозов, получаемых с помощью модели также, как и при бинарной логистической регрессии, служит отрицательное значение 2LL (Удвоенное значение логарифма функции правдоподобия). Разность между начальным значением ("Только постоянное слагаемое") и конечным значением ("Окончательно") указывается в виде значения теста хи-квадрат. которому соотнесен соответствующий уровень значимости. В приведенном примере наблюдается очень значимое улучшение (р < 0,001).
Model Fitting Information (Информация о приближении модели)
|
Model (Модель)
|
-2 Log likelihood (-2 логарифми-ческое правдоподобие)
|
Chi-Square (Хи-квадрат)
|
df (Степень свободы)
|
Sig. (Значи-мость)
|
|
Intercept Only (Только постоянное слагаемое)
|
207,180
|
|
|
|
|
Final (Окончательно)
|
170,408
|
36,772
|
8
|
,000
|
|
Link function: Logit (Связывающая функция: Логит).
|
Для проверки, будут ли наблюдаемые частоты по ячейкам значимо отличаться от ожидаемых частот, рассчитанных на основе модели, выполняется хи-квадрат тест по Пирсону. Его результатом, для данного примера, является не значимая разность значений (р = 0,190), что говорит о достижении высокой степени приближения. Однако, следует обратить внимание на то, что из-за большого количества пустых ячеек применение теста хи-квадрат становится проблематичным.
Goodness of fit (Критерий согласия)
|
|
Chi-Square (Хи-квадрат)
|
df (Степень свободы)
|
Sig. (Значимость)
|
|
Pearson (Пирсон)
|
158,733
|
144
|
,190
|
|
Deviance (Отклонение)
|
127,454
|
144
|
,835
|
Link function: Logit (Связывающая функция: Логит).
Из трёх мер согласия приведенных ниже, мера, вычисленная по методу Нагелькерке (Nagelkerke) является мерой определённости, которая указывает на процентную долю дисперсии, объяснимой при помощи порядковой регрессии, (см. разд. 16.4). В приведенном примере оценка дисперсии составляет 36,7 %.
Pseudo R-Square (Псевдо R-квадрат)
|
Сох and Snell (Кокс и Шелл)
|
,351
|
|
Nagelkerke (Нагелькерке)
|
,367
|
|
McFadden (МакФадден)
|
,138
|
Linkfunction: Logit (Связывающая функция:
Логит).
Результатом анализа являются оценки параметров регрессии приведенные в нижеследующей таблице.
| Parameter
Estimates (Оценки параметров регрессии) |
|
|
Esti-mate (Оце-нка) |
Std. Error (Стандар-тная ошибка) |
Wald (Валь-дов-ский) |
df (Сте-пень сво-боды) |
Sig. (Значи-мость) |
95% Confidence Interval (95 % довери- тельный интервал) |
|
Lower Bound |
Upper Bound |
|
Threshold (Порог) |
[PLAN = 1] |
-,220 |
,968 |
,052 |
1 |
,820 |
-2,118 |
1,677 |
|
[PLAN = 2] |
,981 |
,988 |
,986 |
1 |
,321 |
-,955 |
2,918 |
|
[PLAN = 3] |
2,253 |
1,013 |
4,949 |
1 |
,026 |
,268 |
4,238 |
|
[PLAN = 4] |
3,907 |
1,048 |
13,905 |
1 |
,000 |
1,853 |
5,960 |
|
Location
(Поло-жение) |
[G=1] |
2,145 |
,540 |
15,787 |
1 |
,000 |
1,087 |
3,204 |
|
[G=2] |
1,357 |
,529 |
6,574 |
1 |
,010 |
,320 |
2,394 |
|
[ALTER =1] |
Oa |
, |
, |
0 |
, |
f |
( |
|
[ALTER =2] |
-1,091 |
,433 |
6,355 |
1 |
,012 |
-1,939 |
-,243 |
|
[ALTER =3] |
Oa |
, |
, |
0 |
, |
f |
j |
|
[KDAUER =1] |
1,811 |
,740 |
5,990 |
1 |
,014 |
,361 |
3,261 |
|
JKDAUER =2] |
1,486 |
,782 |
3,606 |
1 |
,058 |
-4.772E-02 |
3,019 |
|
IKDAUER =3] |
1,340 |
,678 |
1 3,905 |
1 |
,048 |
1.101E-02 |
2,669 |
|
[KDAUER =4] |
Oa |
, |
, |
0 |
, |
( |
, |
|
[SCHULE =1] |
-1,183 |
,618 |
3,665 |
1 |
,056 |
-2,394 |
2.807E-02 |
|
[SCHULE =2] |
-,659 |
,700 |
,886 |
1 |
,347 |
-2,031 |
,713 |
|
rSCHULE =31 |
Oa |
|
|
0 |
|
|
|
Link function: Logit (Связывающая функция: Логит).
a. This parameter is set to zero because it is redundant (Этот параметр приравнен к нулю, так как является дублирующим). !
Каждой категории зависимых переменных и каждой категории факторов сопоставлена оценка параметра регрессии, причём оценки для соответствующих категорий высших
порядков являются дублирующими и поэтому приравнены к нулю. Оценки параметров регрессии для зависимой переменной являются пороговыми оценками, которые для факторов называются оценками положения.
Оценки положения дают возможность толковать влияние факторов и указывают на степень этого влияния. Поэтому, прежде чем будет продемонстрирована точная математическая связь между факторами влияния и зависимой переменной, можно констатировать следующее:
-
Из таблицы можно узнать, какие из факторов вообще оказывают значимое влияние на зависимую переменную. Такими факторами являются возраст, пол и продолжительность болезни, в то время как образование находится на самой границы значимости, до перехода этой границы осталось совсем не много.
-
Положительные оценки означают, что
соответствующая категория действует в качестве высшей категории зависимой переменной; отрицательные оценки указывают на действие в качестве низших категорий зависимых переменных.
Принадлежность к младшим возрастным группам является причиной более единодушного одобрения предложения: "Разработать план лечения и затем приступать к его воплощению", все мужчины менее склонны к такому предложению, небольшая продолжительность болезни, а также высокое или низкое образование ведут к снижению степени одобрения. Это соответствует результатам корреляционного анализа.
Математическое значение оценок параметров регрессии заключается в том, что на них основе могут быть вычислены кумулятивные (суммарные) вероятности для категорий независимых переменных. Покажем это на конкретном примере.
Для этого возьмем в редакторе данных первого пациента и рассчитаем совокупную вероятность для случая, когда он отмечает одну из первых двух категорий ("gar nicht" (абсолютно не верно) или "wenig" (слабо)) для зависимой переменной.
Первый пациент является мужчиной средней возрастной группы с большой продолжительностью болезни и неполным средним образованием. Учитывая все эти сведения, можно ожидать высокую вероятность того, что больной проявит слабую готовность планомерно лечить свою болезнь.
На первом шаге расчёта мы должны сложить оценки положения, соответствующие отдельным категориям:
|
alter = 2
|
1,347
|
|
g = 1
|
-1,091
|
|
Kdauer = 4
|
0,000
|
|
Schule = 1
|
-1,183
|
|
Сумма
|
-0,917
|
Эту сумму нам теперь нужно отнять от пороговой величины второй категории зависимой переменной (plan = 2):
0,981 - (-0,917) = 0,981 + 0,917 = 1,898
Как можно заметить по значению, которое превосходит единицу, этот показатель пока ещё не является искомой совокупной вероятностью того, что больной отметит одну из первых двух категорий. Значение этого показателя соответствует связующей функции, приведенной к этой вероятности. В нашем примере мы выбрали в качестве связующей логит-функцию, установленную по умолчанию, так что для искомой вероятности справедливо следующее выражение:
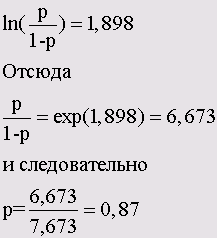
Таким образом, вероятность того, что первый пациент отметит одну из первых двух категорий, составляет р = 0,87 или 87 %. Фактически пациент отметил категорию 1.
Чтобы успокоить пользователей программы, следует сказать, что Вы можете избежать этих сложных расчётов. В диалоговом окне Ordinal Regression:Output (Порядковая регрессия: Вывод) мы активировали опцию сохранения некоторых переменных, которые теперь можем просмотреть.
Пять переменных est1_1-est5_1 соответствуют вероятностям для пяти категорий зависимой переменной. Если мы возьмем первого пациента, то достаточно сложить вероятности для первых двух категорий:
0,67 + 0,20 = 0,87
Это соответствует тому значению, которое мы рассчитали для совокупной вероятности второй категории. В переменной рге_1 сохранен номер категории, которой соответствует самая высокая вероятность, названная "прогнозируемой категорией". Переменная рср_1 ещё раз дает вероятность выбора этой категории.
Связующая логит-функция выбранная нами для этого примера, принадлежит к набору из пяти функций, приведенных ниже.
|
Функция
|
Форма
|
Применение
|
|
Logit (Логит)
|
In (р/(1-р))
|
Равномерно распределённые
категории
|
|
Complementary log-log (Сопряженный двойной логарифм)
|
ln(-ln(1-p))
|
Высшие категории представлены сильнее
|
|
Negative log-log (Отрицательный двойной логарифм)
|
-ln(-ln(p))
|
Низшие категории представлены сильнее
|
|
Probit (Пробит)
|
Инверсия стандартного комулятивногонормального
распределения
|
Нормально распределённые
частоты
|
|
Cauchit (Коши)
|
tan(7t(p-0.5))
|
Появление пиковых значений
|
В качестве меры качества прогнозирования можно использовать ранговую корреляцию по Спирману между фактически наблюдаемой категорией (переменная plan) и прогнозируемой категорией (переменная рге_1). Для приведенного примера (связующая функция — логит) получим г = 0,611; для других связующих функций получаются более низкие значения.
Лучшую модель можно получить, если в диалоговом окне Ordinal Regression: Location (Порядковая регрессия: Положение) наряду с главными эффектами включить и взаимодействия. После активирования опции Custom (Пользовательский режим) в вашем распоряжении появляется вспомогательное меню, при помощи которого вместе с главным эффектом Вы сможете включить в модель и различные виды взаимодействия.
-
Активируйте опцию Custom (Пользовательский режим) и сперва выберите в появившемся списке Main effects (Главные эффекты).
-
При помоши транспортной кнопки перенесите все факторы в поле Location model: (Определение положения для модели).
-
Затем отметьте в разворачивающемся меню Interaction (Взаимодействие) и повторно перенесите все факторы в поле Location model: (Определение положения для модели). Будет выбрано взаимодействие четвёртого уровня. При помоши опции All 2-way (Все дважды) Вы можете задать взаимодействие второго уровня, при помощи опции АН З-way (Все трижды) — взаимодействие третьего уровня и т.д.
Теперь прогноз будет лучше; в случае применения для данного примера взаимодействия четвёртого уровня ранговая корреляция между наблюдаемой и прогнозируемой категориями возрастает с 0,611 до 0,739. При этом, конечно же, возрастает и количество параметрических оценок.
|